【人気ダウンロード！】 円 体積 求め 方 628680-円 体積 の 求め 方

 円柱の体積の求め方＝半径×半径×円周率×高さ 円柱に関して、体積を求める問題がよく作られます。 たとえば上の写真のように、底の円の半径と円柱の高さが示されて「この円柱の体積を求めよ」と問われます。 上の情報を元に計算の流れを説明して 1L（リットル）＝1000㎤ つまり、求めた体積 (㎤)を÷1000するとリットルの単位に変換することができます。 この円柱には096 (L)の水が入ることが分かりました。 円柱の中に何リットルの水がという問題では、体積を求めた後の÷1000がポイントになります7174円 各種立体の特徴や性質、体積の求め方の指導に！ 期間限定ポイント10倍透明立体模型 17種 オレンジ（大） おもちゃ 知育玩具・学習玩具 かず・計算 7174円 各種立体の特徴や性質、体積の求め方の指導に！

地図の体積計測

円 体積 の 求め 方

円 体積 の 求め 方- 円柱の体積の求め方 円柱の体積の求め方に関しては、三角柱などの体積の求め方と変わりません。 〇〇柱の体積は、全て (底面積)×(高さ) で求まると覚えていて良いです。 円柱の場合でも、底面積が円になるだけで特に難しくはありません。 後の練習問題で具体的に確認をしましょう！3) 円柱面x2 y2 = a2 の円柱面x2 z2 = a2 の内部にある部分の曲面積を 求めよ。 4) xy 平面上のC1 級曲線y = f(x) (a • x • b) をx 軸のまわりに1回転 してできる曲面の曲面積は S = 2 Z b a jf(x)j p 1(f0(x))2dxとなることを証明せよ。 5) 曲面z = Arctan(y=x) (x;y > 0) の円柱面x2 y2 = a2 の内部にある部 分の曲面積を

１つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

 小学6年生で習う、円の面積の問題の解き方を世界一やさしく解説します。 ★今から学ぶこと 1、円の面積を求める式円の面積=半径×半径×314 2、円の一部の面積を求める式円の面積の一部=半径×半径×314×中心の角/360° 3、色（かげ）がついた部分の面積の求め方全体白い部分の体積 V = πr2h V = π r 2 h 体積 = 半径 × 半径 × 314 × 高さ 公式の 導出 ( どうしゅつ ) 方法と計算例は、「 円柱の体積の求め方 」をご覧ください。 円柱の体積の求め方 高校数学 kanrinin 微分でつなげる円や球の公式 今回の内容の動画版です→球の体積公式の微分が表面積になっている理由 円の面積、円周の長さおよび球の体積、表面積は次のように計算できます。

 円の面積、円柱の体積と比重 18年10月14日 年6月28日 sho U 「半径×半径×π」が、学校で習った基本的な円の面積の求め方でした。しかし、社会に出てみると意外とそれ以外の方法もあることを事を知りました。楕円の面積と楕円体の体積の求め方 korokoro 年10月7日 こんにちは（ @t_kun_kamakiri ）。 さてこの記事を読みに来た方は、「楕円の面積や体積の公式」を求めてきたことだと思います。 あるいは、楕円の面積や体積の公式はどうやって導かれるのかと知り 円柱の体積＝7×7×314×12＝（cm³）となります。 答え 円柱ができる。 体積はcm³ ～立体の体積・表面積を求める公式まとめ～ 立方体・直方体の体積の求め方公式 円柱の表面積の求め方公式 三角柱の体積の求め方公式 円錐の体積

円柱の体積（ V olume） S 底面の面積（ S urface area） h 高さ（ h eight） π 円周率（= 314） r 底面の円の半径（ r adius） 斜円柱の体積の求め方 ここからは、補足的に直円柱と斜円柱について述べ 円の面積はなぜ「π×r×r」なのか？ – 公式の求め方を丁寧に解説 円の面積の公式はなぜ「××」と表現できるのでしょうか？ ここではそんな疑問に対して、図形を使った簡単な公式のイメージ方法を紹介します。 先に言っておくと、ここで紹介する方法円柱の体積＝底面の面積×高さ より， 体積は，4π×2＝8π(cm3)となります。 このように，回転体の体積を求めることは中学1年で学習しますが，上の方法とまったくちがう求め方があ ります。その方法を紹介しましょう。

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

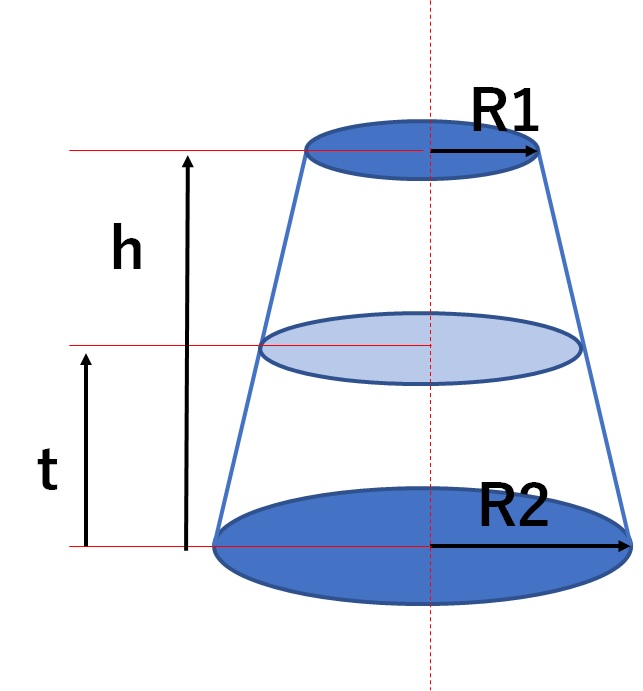
円錐台の体積を半分にする高さを計算 高精度計算サイト

 うさぎでもわかる解析 Part27 2重積分の応用（体積・曲面積の求め方） 19年11月4日 21年7月16日 49分1秒 ももうさ スポンサードリンク こんにちは、ももやまです。 今回は2重積分を使って立体の体積や曲面積（表面積）を求める方法についてまとめてい円の面積 円の面積 4分割 解説 円の面積 8分割 解説 円の面積 16分割 解説 円の面積の求め方 解説 円柱の体積 円柱の体積の求め方 円 円は2通りの求め方を紹介します。ここで求めたい円の面積の半径を\(r\)としておきます。 パターン① 1つ目の求め方についてです。 円の面積を求めたいので、 円がどのような線の集まりでできているか を考える必要があります。

円柱の体積の求め方 公式 小学生 中学生の勉強

球の体積の公式 求め方や覚え方のコツを紹介するよ 中学や高校の数学の計算問題

まずは円柱の体積の求め方底面積πr^2×高さ2rを援用。 幅 rΔΘ で刻まれた 球の断層 πr^2*cos(Θ) を π/2 から π/2 にかけて積層したイメージ、ないしは 球の断層 πr^2*sin(Θ) を 0 から π にかけて積層したイメージに到達する。表面積の証明1 球の表面積を積分で直接求めに行きます。 \theta\Delta \theta θ Δθ の部分（帯のような図形※）の表面積を考える。 ※イメージするのが難しい方は，地球儀を持ってきて「緯度が30度から31度の間の部分（帯）」を考えてみてください。 帯は 円錐の体積の求め方の公式って？？ こんにちは、この記事をかいているKenだよ。犬の散歩が趣味だね。 円錐の体積の求め方の公式は、 底面積×高さ×1/3 だったよね。 もう少し詳しくかいてあげると、 半径×半径×円周率×円錐の高さ×1/3 になるんだ。

中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室

1

 円の面積の求め方 円の面積を求めるときは 円の面積 = 半径 × 半径 × 円周率 という公式を使います。 たとえば、半径が 3 c m の円の面積は 半径 半径 円周率 半 径 × 半 径 × 円 周 率 = 3 × 3 × 314 = 26 c m 2 と求めることができます。 Tooda Yuuto 「なんで3つの領域のうち、求めたいものを隠せば公式が得られます。 例えば、質量を求めたい場合、質量を隠すと、 体積×密度 となります。 はじきの法則（速さ、時間、距離の公式）をこのような図で覚えた人も多いでしょう。体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱（管） 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

円錐の体積ってなんであの公式なの Webty Staff Blog

円柱の体積、表面積の求め方はこれでバッチリ！←今回の記事 円錐の表面積、中心角の求め方を解説！裏ワザ公式も！ 円錐を転がすと1周するのにどれくらい回転する？ 球の体積・表面積の公式はこれでバッチリ！語呂合わせで覚えちゃおう！球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半直方体の体積の公式は？1分でわかる求め方、例題、直方体の面積の公式 円柱の体積 円柱とは下図に示す図形です。底面が円形なので、底面積は円の面積を求めます。円の面積に高さを掛けた値が円柱の体積です。 よって、 円柱の体積＝3×3×314×5＝1413cm

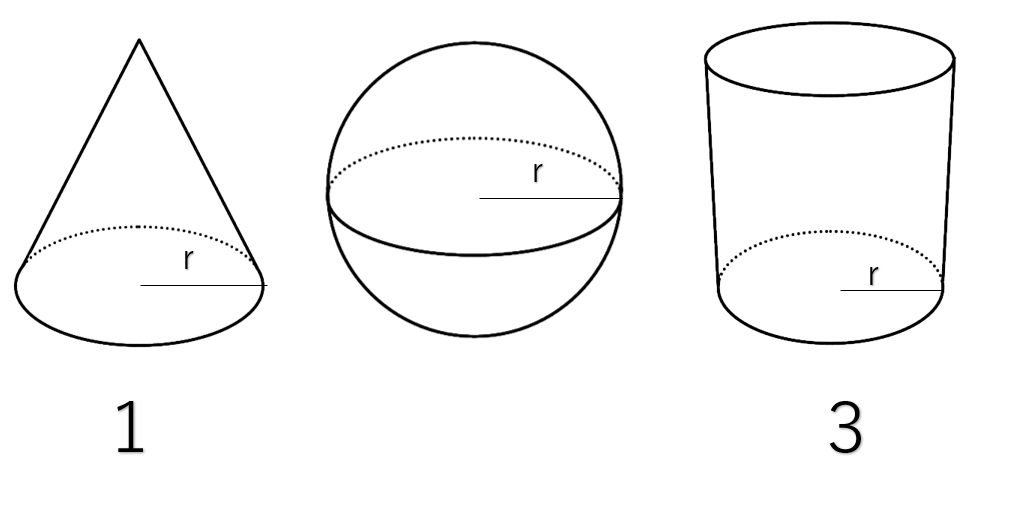
中１ 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾

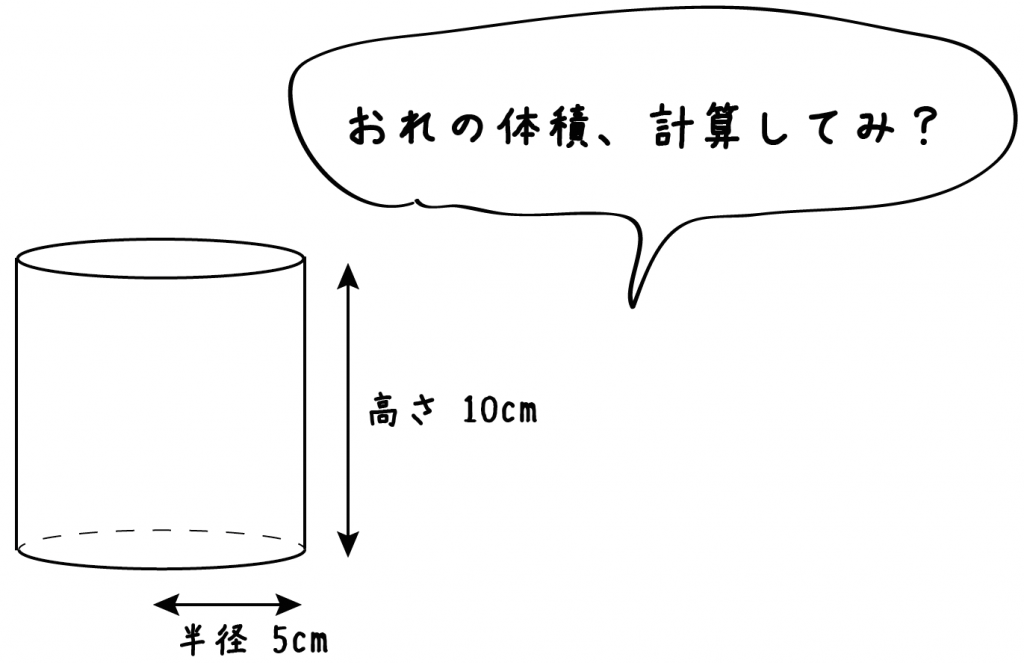
計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

 目的 「楕円の面積」や「楕円体の体積」の求め方を紹介します。 理解のためのステップ ステップ ステップとして下記のステップを踏んで「4楕円体の体積」を求めたいと思います。 1円の面積 2楕円の面積 3球の体積直円柱の体積 そういえばこんな公式でしたね。 ケーキ型をHPに載っているものと違うものを使うにあたって、体積を知りたかった。 計算式は知っているけれどもこうやってあるととっても便利でした。 半径よりは直径のほうがいい気がしますが、普通に小学生の算数・図形・面積・体積に関する算数の問題プリント、練習プリントです。 無料でダウンロード、印刷してご利用いただけます。 小学1年生の算数 図形 練習問題プリント 小学2年生の算数 図形 練習問題プリント 小学3年生の算数 図形 練習問題

3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ

三平方の定理 円錐の高さが 体積を求める問題を解説 数スタ

 円柱の体積の求め方 はむちゃくちゃ簡単。 底面積×高さ っていう公式をつかえば、一発で体積を求めることができるんだ。 そんで、 底面積は、 半径×半径×円周率 だから、円周の体積はつぎの計算式で求められるよ。 半径×半径×円周率×高さ 円の面積の求め方と覚えるコツ。 なぜ半径×半径×314になるか 円の面積は、 「半径 × 半径 × 314」 （半径 × 半径 × 円周率 π ）という公式で求めることができます。 例題①半径 2 cmの円の面積を求めて下さい。 例題②半径 5 cmの円の面積を求めて下さい3、球の体積の求め方 円の面積の初等的な求め方は簡単だ。 でも、そこには積分の初期的な概念がある。 では、その初歩的な概念から積分へはどうやって至るのだろうか。 その積分を身体で感じるために、簡単に求まる円の面積を積分で求めてみよう。

地図の体積計測

１つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

 《円の直径の求め方》 円周＝直径×314＝4396 であることから 答え 14cm 《円の面積の求め方》 円の直径が14cmとわかったので、半径はその半分の7cm。 よって、この円の面積は半径×半径×314より 答え ㎠ 問題④ この鉄の円注の重量（重さ）を計算してみましょう。 解答1 上の換算式を元に重量計算していきます。 このとき、計算しやすいようにまずはmmからcmへ換算しておくといいです。 10mmが1cmであることから、30mm＝3cm、0mm＝cmとなります。 すると、314 ×

中１数学 円柱の体積 表面積はどうやって求めるの まなビタミン

角柱 円柱の体積の公式 小学生に教えるための分かりやすい解説 数学fun

1

簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

円錐 完全攻略 体積 弧の長さ 中心角 側面積 表面積 母線の長さ 教遊者

立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者

1

円錐とは 体積 表面積の公式や求め方 受験辞典

円柱の体積の求め方 公式 小学生 中学生の勉強

算数の問題です 1 図の立体は 円柱を半分に切った形です この立体の体積は何 Yahoo 知恵袋

計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

円錐の表面積の求め方 公式と計算例

角錐 円錐の体積と表面積の公式 数学fun

計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ

半径5分の12cm 高さ6cmの双円錐の体積を求めるのに Clearnote

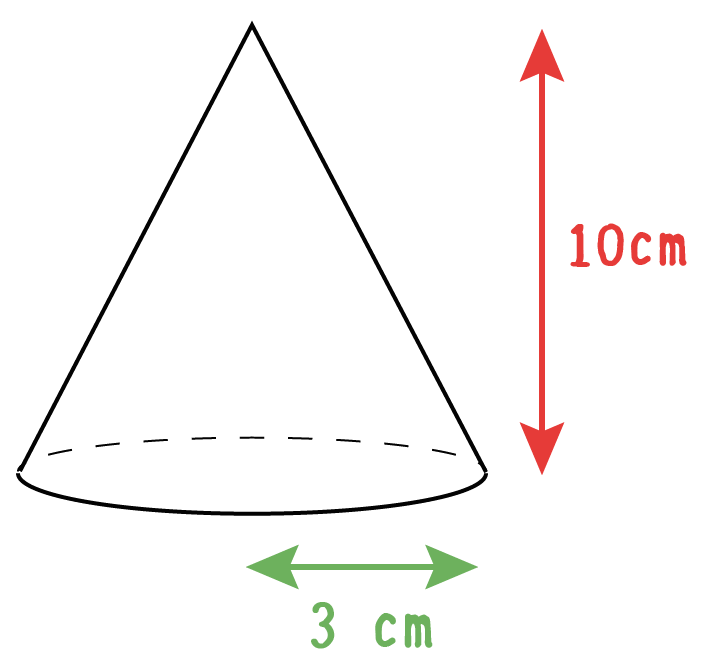
計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

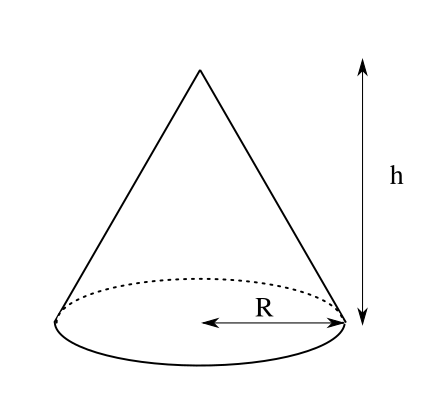
円錐の体積を円柱座標系で真面目に計算してみた ゴルディアスの涙目

円柱の体積の求め方 公式 小学生 中学生の勉強

体積比の求め方が分かりません Clearnote

空間図形 角柱 角錐 すい 円柱 円錐の体積の求め方 中学数学 定期テスト対策サイト

簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく

円錐や三角錐の体積比の求め方 相似比 辺の長さの比から計算 白丸くん

うさぎでもわかる解析 Part27 2重積分の応用 体積 曲面積の求め方 工業大学生ももやまのうさぎ塾

算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ

円錐の体積ってなんであの公式なの Webty Staff Blog

丸棒の重量 円柱の体積と重量の求め方 鉄の場合

中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学

円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典

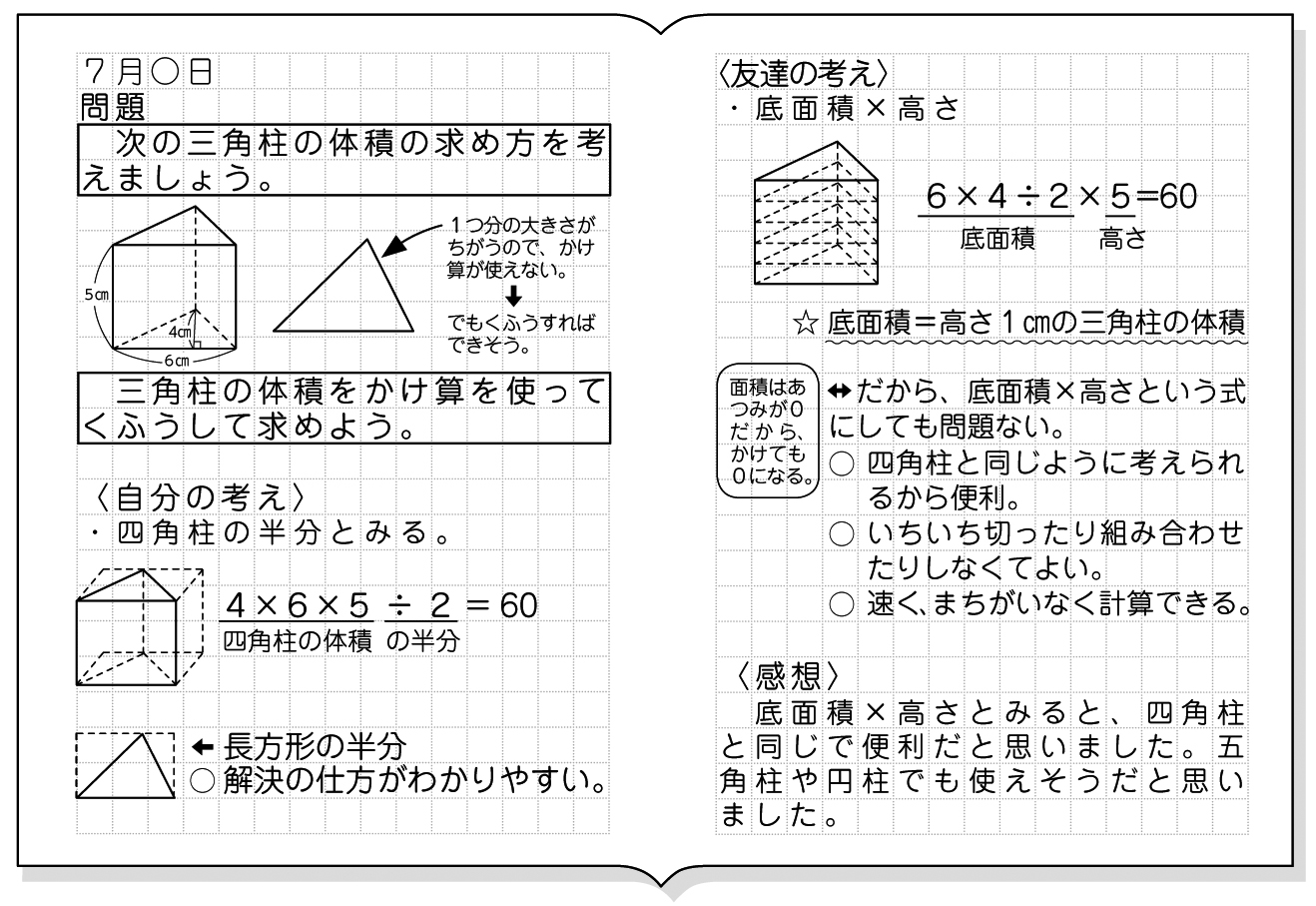
小6算数 角柱と円柱の体積 指導アイデア みんなの教育技術

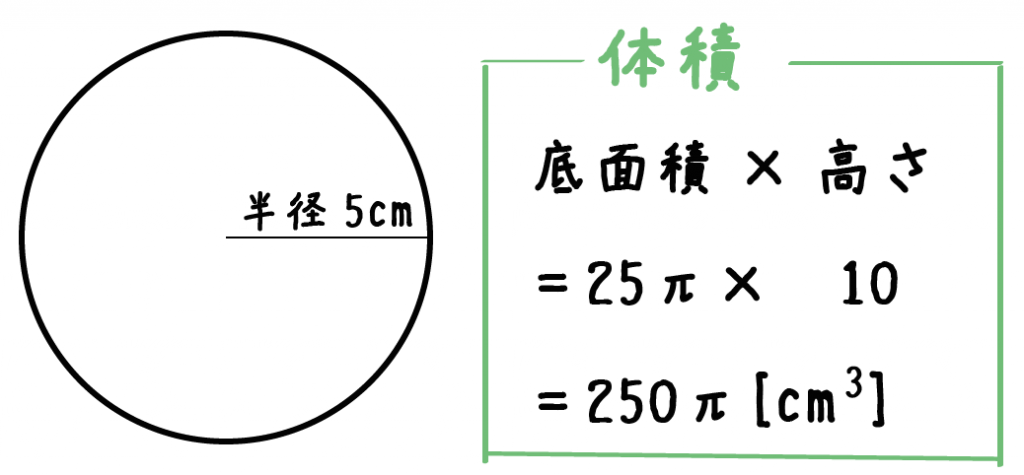
計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

簡単公式 円柱の表面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

円柱の容積は 1分でわかる意味 求め方と式 表面積の計算 体積と直径の関係

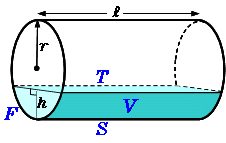
一部が欠けた直円柱の体積 高精度計算サイト

簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく

半球の体積と表面積を計算する 具体例で学ぶ数学

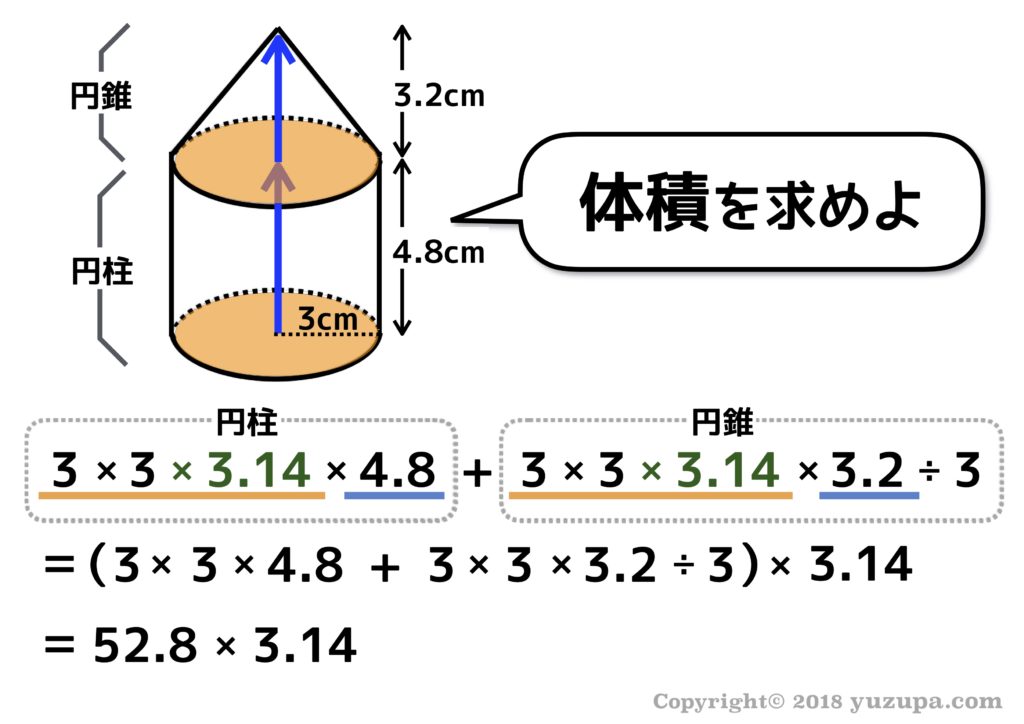
中学受験 円周率暗記プリント 体積問題で間違いを連発する２つの理由 かるび勉強部屋

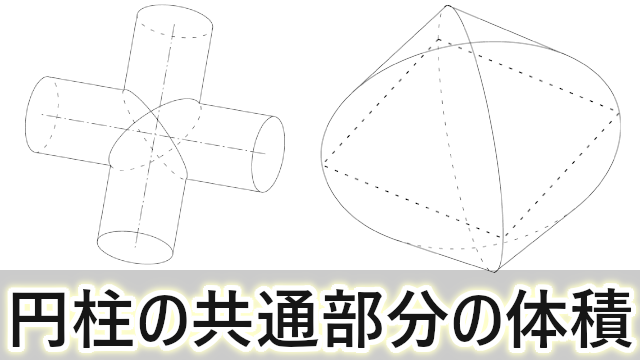
円柱の共通部分の体積 非回転体の体積 大学入試数学の考え方と解法

積分計算による体積の求め方 断面積の積分や回転体の体積 受験辞典

円錐の体積と公式は 1分でわかる公式 問題と高さの求め方 証明

円柱の表面積と体積を求める公式 具体例で学ぶ数学

計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

中１数学 円柱の体積 表面積はどうやって求めるの まなビタミン

計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

中学数学 円錐の表面積の求め方と公式 図たくさん なぜか分かる はかせちゃんの怪しい研究室

球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ

球の表面積と体積の公式 数学fun

円柱の体積の求め方 公式と計算例

立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者

1

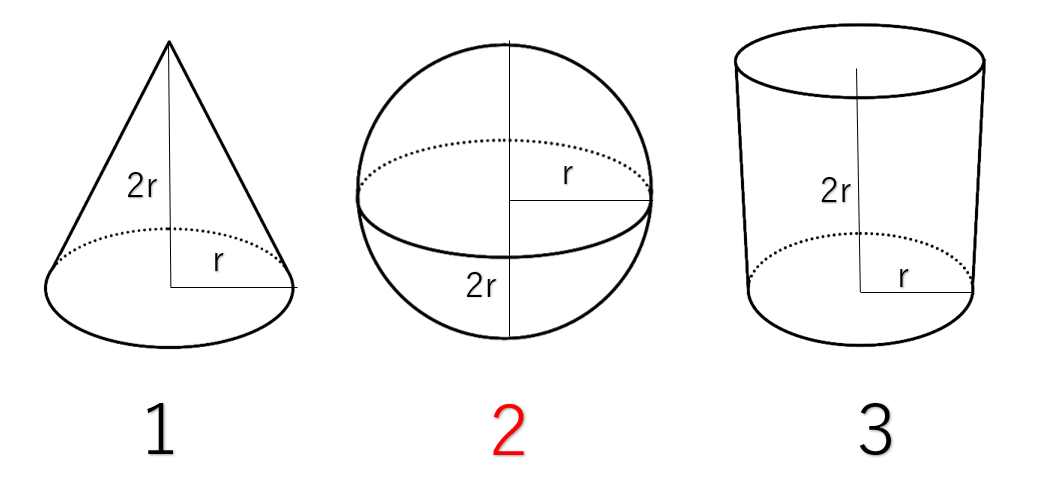
中１ 数学 暗記に頼らない 球の体積の求め方 こいがくぼ翼学習塾

中学数学 円柱の体積の求め方と公式 塔をモチーフ なぜか分かる はかせちゃんの怪しい研究室

円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学

2

質量と比重

円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題

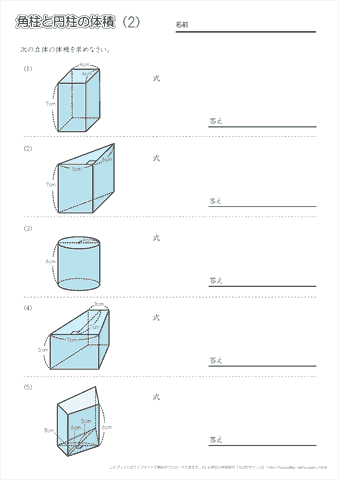
小学６年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生

円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題

円錐の体積を求める Youtube

空間図形14 円すい台の体積 Youtube

中1 数学 6 5 球の体積 表面積 Youtube

円すい 円錐 の体積の求め方と問題 小学数学 Irohabook

公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ

球の体積と表面積の求め方 公式を使う中学数学での計算 リョースケ大学

簡単 円柱の体積公式は底面積 高さ 必ず解きたい計算問題付き 高校生向け受験応援メディア 受験のミカタ

球の体積と表面積 公式と計算問題と証明 Irohabook

円錐の体積の求め方 公式と計算例

球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典

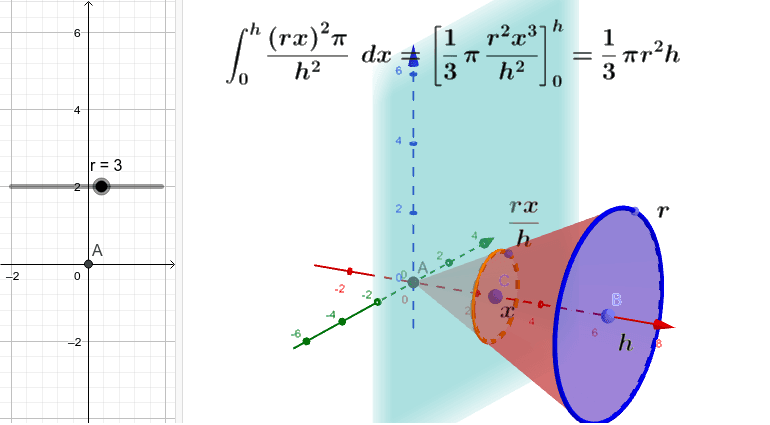
円錐の体積の求め方 Geogebra

円柱の計算 体積 表面積の求め方はこれでバッチリ 数スタ

3分でわかる 円錐の体積 表面積の求め方 合格サプリ

角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学

3分でわかる 円錐の体積 表面積の求め方 合格サプリ

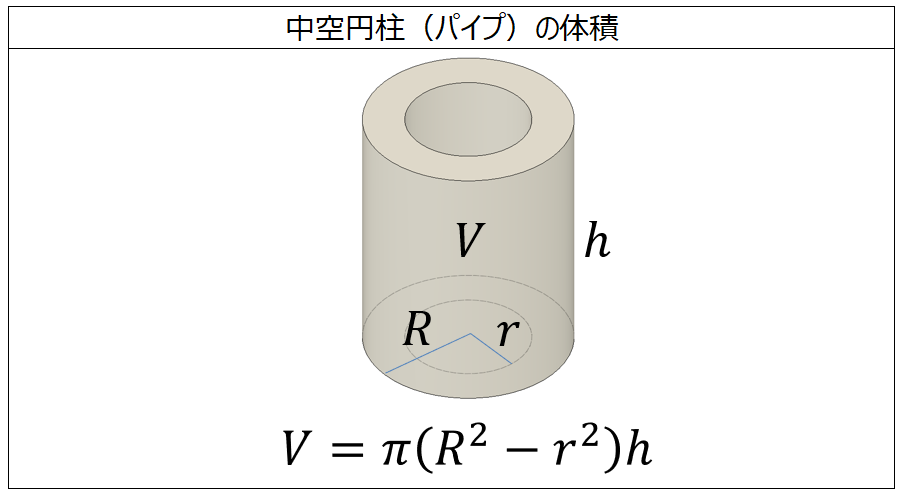
体積の計算 中空円柱 パイプ 製品設計知識

2 を途中式を含めて教えてください Clearnote

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

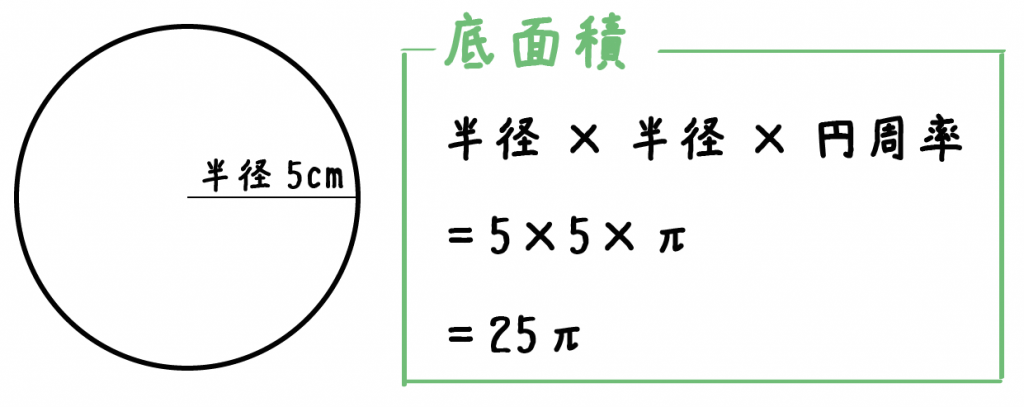
計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題

公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ

円柱の表面積と体積を求める公式 具体例で学ぶ数学

中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室

円錐 体積の比較 中学から数学だいすき

球の体積と表面積 Youtube

１つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード

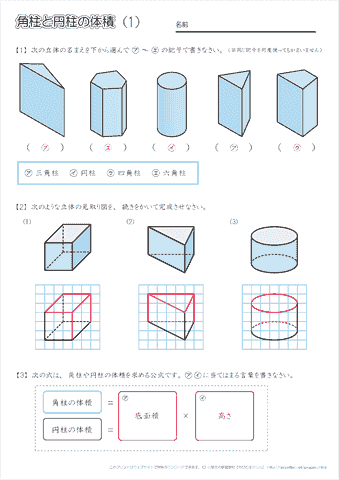
小学６年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生

中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく

毎日問題を解こう 27 苦手な数学を簡単に

中3 三角形の相似 円錐の体積比 日本語版 Youtube

Incoming Term: 円 体積 の 求め 方,